Content
- Definition of Radioactive Minerals
- Table of Naturally Occurring Radioactive Isotopes
- Caveats, Disclaimers, and Warnings
- Precautions for storing radioactive minerals
- Caveats on the Calculation of radioactivity in minerals
- Calculation of Radioactive Activity
- Electron Density
- Photo-Electric Effect
- Gamma Ray (API Units)
- Radiation Dose Estimation
- Tables of Radioactive
Isotope Activities
- Table 1A (238U) Uranium Decay Series
- Table 1B (235U) Actinium Decay Series
- Table 2 (232Th) Thorium Decay Series
- Table 3 All other Significant Isotopes
Radioactivity in minerals are caused by the inclusion of naturally-occurring
radioactive elements in the mineral's composition. The degree of radioactivity
is dependent on the concentration and isotope present in the mineral. For the
most part, minerals that contain potassium (K), uranium (U), and thorium
(Th)
are radioactive. This table lists all of the
naturally-occurring radioactive isotopes.
Mineral radioactivity is due to alpha, beta, and gamma radiation from the
unstable isotopes in the composition. Alpha decay is due to the ejection of a helium
nucleus (2 protons and 2 neutrons) from
the parent isotope. This alpha particle is accompanied
by gamma radiation and a daughter isotope which is two protons and two neutrons
lighter than the parent isotope. Beta decay is due to the ejection of an
electron from a neutron in the parent nucleus. This particle is accompanied by
gamma radiation and a daughter isotope which is one proton heavier and one
neutron lighter than the parent isotope. Electron Capture (EC) decay is
very rare and is the result of the nucleus capturing one of the atom's orbital
electrons. This decay is accompanied by gamma radiation and a daughter
isotope which is one neutron heavier and one proton lighter than the parent
isotope.
Of the three main types of radioactive decay, gamma radiation causes the most
damage because it has a greater effect on biological materials and is
neutralized only by heavy shielding. The next most damaging type of radiation is
beta particles which is absorbed by a few feet of air. The least damaging is
alpha particles which has a range of 6 inches or less in air.
Table of Naturally Occurring Radioactive Isotopes
| Element |
Isotope
Symbol |
Natural Abundance |
Half-life (Years) |
Primary Decay Mode |
|
Tellurium |
130Te |
33.97% |
2,400,000,000,000,000,000,000.00 |
|
| Vanadium |
50V |
0.25% |
390,000,000,000,000,000.00 |
EC |
|
Zirconium |
96Zr |
2.80% |
360,000,000,000,000,000.00 |
|
|
Samarium |
149Sm |
13.80% |
10,000,000,000,000,000.00 |
alpha |
|
Samarium |
148Sm |
11.30% |
7,000,000,000,000,000.00 |
alpha |
|
Osmium |
186Os |
1.58% |
2,000,000,000,000,000.00 |
alpha |
|
Neodymium |
145Nd |
8.30% |
1,100,000,000,000,000.00 |
alpha |
|
Platinum |
192Pt |
0.79% |
1,000,000,000,000,000.00 |
alpha |
|
Indium |
115In |
95.70% |
600,000,000,000,000.00 |
beta - |
|
Gadolinium |
152Gd |
0.20% |
110,000,000,000,000.00 |
alpha |
|
Tellurium |
123Te |
0.89% |
13,000,000,000,000.00 |
EC |
|
Platinum |
190Pt |
0.01% |
690,000,000,000.00 |
alpha |
|
Samarium |
147Sm |
15.00% |
108,000,000,000.00 |
alpha |
|
Rubidium |
87Rb |
27.83% |
49,000,000,000.00 |
beta - |
|
Rhenium |
187Re |
62.60% |
45,000,000,000.00 |
beta - |
|
Lutetium |
176Lu |
2.59% |
22,000,000,000.00 |
beta - |
|
Thorium |
232Th |
100.00% |
14,000,000,000.00 |
alpha |
| Uranium |
238U |
99.28% |
4,460,000,000.00 |
alpha |
| Potassium |
40K |
0.01% |
1,250,000,000.00 |
beta - |
| Uranium |
235U |
0.72% |
704,000,000.00 |
alpha |
| Significant Radioisotopes |
Caveats, Disclaimers, and Warnings
Radioactive minerals emit alpha, beta and gamma radiation. The amount
of that radiation is best measured with Geiger counters or scintillation
counters. Warning: If you collect or possess radioactive minerals, you really should have
a means of measuring radiation to determine if the extraordinary precautions are
needed to store the mineral. If you don't have such equipment, inexpensive
track-etch (Radon)
detectors are a good way to determine if there is a danger. Get three detectors,
place one in your mineral cabinet, the next in the room which houses the
collection and the third as a blank to check on the laboratory that processes
the detectors. The EPA limit on indoor radon
exposure is 4 pCi/liter of air.
Precautions for storing radioactive minerals are as follows:
- Handle the specimen as little as possible. A good strategy is to place
the specimen in a transparent container which is sealed. Wash your hands
after handling the specimen.
- Do not smoke, eat, or sleep near the specimens.
- Limit the specimen size since exposure is related to the amount of
mineral present.
- Secure the specimen from children or curious adults.
- Alpha and beta radiation is absorbed by a coupe of feet of air or by a
glass cabinet window. Gamma radiation is not.
- The main environmental exposure hazard from radioactive minerals comes from the
buildup of Radon
gas emitted by Uranium- and Thorium- bearing minerals. Museums who display
large radioactive specimens provide vents to the outside. A good strategy
for personal collectors is to place a cheap aquarium pump inside a closed
mineral cabinet. Route the output of the pump to the outside.
The calculation of radioactivity in minerals is dependent on certain
assumptions which affect the true activity of a mineral. The assumptions used in
calculating mineral radioactivity are:
- Uranium (238U
& 235U) and
Thorium (232Th)
decay produces a series of daughter isotopes which are themselves
radioactive. The calculation assumes full secular-equilibrium with the daughter
isotopes. Branching decay modes are ignored.
- The isotopic composition is estimated from the natural
abundance of the radioactive isotope in the element. It is
assumed that no isotopic fractionation of the element has occurred in the
specimen.
- Minerals which contain Rare Earth Elements (REE) are generally more
radioactive because thorium is commonly substituted for one or more of
these REE. If thorium is not accounted for in the empirical formula, then
thorium is added to the total activity by using the relationship % Th =
S % REE x 0.05.
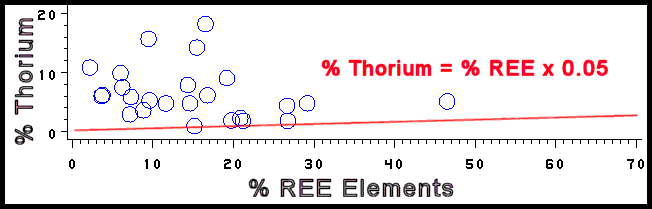
This is a general relationship and is probably too high for carbonate and
phosphate REE minerals and too low for silicate REE minerals.
- Radioactive accessory minerals such as zircon may contribute to the
radioactivity of a mineral which is otherwise non-radioactive by
calculation. Many granites or other igneous rocks contain some
radioactivity because of minor, but highly radioactive, accessory
minerals.
Activity of a given amount of radioactive material found in nature is calculated as the decay constant l (related to the half-life T) multiplied by the number of radioactive nuclei. One kilogram of
naturally-occurring element with X percentage of radioactive isotope with half-life T[sec] has activity R[Bq/kg]:
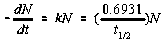
where N = 6.023┤1023 the Avogadro
number times 1,000 gm/Isotope Mass times the % Abundance, ln 2 = 0.693, and T is the half-life in seconds.
The unit of activity is Becquerel (1 Bq = 1 decay/sec) or Curie (1 Ci = 3.7┤1010 Bq).
kN is therefore, the activity of 1 kg of element with x percent of radioisotope
in counts/sec. These values are multiplied by the chemical composition for each
element in the empirical formula of
the mineral to determine the theoretical radioactivity of that mineral.
note: The origin of the Curie unit was based on the
activity of 1 gram of 226Ra.
| Element (Natural
Isotopic Abundance) |
Activity (Becquerels/kg) |
Source |
| Uranium (U) |
179,000,000 |
Table 1A, 1B |
| Thorium (Th) |
44,800,000 |
Table 2 |
| Potassium (K) |
30,316 |
Table 3 |
| Lutetium (Lu) |
48,500 |
Table 3 |
| Rhenium (Re) |
1,020,000 |
Table 3 |
| Rubidium (Rb) |
891,000 |
Table 3 |
| Samarium (Sm) |
127,000 |
Table 3 |
| Rare Earth Elements (REE) |
8,044 |
Estimated |
Gamma rays from all this activity pass through the mineral and
experience successive Compton-scattering collisions with the mineral's
atoms. Each collision reduces the the energy of the gamma ray until it is
absorbed by the photo-electric effect. The rate of absorption varies with
the electron density (re) of the mineral. Higher Z atoms (high electron density) have
a greater adsorption factor than low Z atoms (low electron density). The end
result from all this self-adsorption is the apparent radioactivity observed for
the mineral specimen is much less than the absolute activities calculated by the
rate equation.
Electron density of the mineral is calculated as follows:
re = mineral density (S Atomic
number / Molecular Weight)
where re is the electron density in
grams/cc.
Photo-electric absorption effect is calculated from the following relationship:
Pe = (Z3.6/10)*0.0025 where:
Z = Atomic number of the atom and Pe has the units of
barns/electron.
Pemin = S Ai Zi Pi / S Ai Zi where:
Ai
= atomic number atom (i) in the mineral, Zi = atomic number
atom (i), Pi = Pe value of atom (I).
U = Pemin * re where:
U is the photoelectric effect in barns/cc
Gamma Ray (GR) response for the mineral is estimated by taking the bulk activity
calculation and correcting for absorption and density by comparing the gamma ray
measurements derived from the geophysical log response (borehole geometry)
from the American Petroleum Institute test
facility in Houston, Texas:
GRapi = Bq/21 x 2 (S Z/mole wt.) where:
GRapi is gamma ray (in api units), 210 is the empirical
proportionality factor from Bq to GRapi units, and Z = mean atomic number of
the mineral.
Definitions of Radiation Dose Measurements (see Natural
Sources of Ionizing Radiation).
-
A rad, or "radiation absorbed
dose," is a unit of absorbed dose equivalent to the deposition
of 100 ergs of energy per gram of tissue
-
A rem, or "roentgen equivalent
man," is a unit of absorbed dose that takes into account the relative
biological damage caused by the various ways that ionizing radiation
deposits its energy in tissue
-
A roentgen (abbreviated "R" and
pronounced "rent-gen") measures gamma and beta radiation dose
based on the amount of ionization in the air.
Radiation Dose Calculation is based on the
GRapi response. Since the GRapi response is scaled to the borehole
geometry where the detector is centered in a borehole with a 3 inch
standoff, the estimate is based on the GRapi response of common clay
minerals. The government estimated exposure to terrestrial sources is 30
mRem/year. If you hold a 1 kg sample, 1/2 the ratioactivity is absorbed in
your hand and 1/2 radiates away in the other direction. Therefore using 200
GRapi as background of 15 mrem/year:
mRem=(GRapi/200)/(365*24) where:
mRem/hr exposure is related to a 1 kg of the mineral held for one hour.
Table 1A: Uranium decay series
| Isotope |
Half-life |
Half-life
Units |
Half-life
Seconds |
Decay |
N
(mole/kg)*
%Abundance |
Calculated
Activity (Becquerel)
Kg-sec |
Calculated
Activity (Curie) Ci/Kg-sec |
Decay
Energy (MeV) |
| 238U |
4.47E+09 |
years |
1.41E+17 |
a |
2.512E+24 |
1.236E+07 |
3.340E-04 |
4.270 |
| 234Th |
2.41E+01 |
days |
2.08E+06 |
b- |
3.713E+13 |
1.236E+07 |
3.340E-04 |
0.273 |
| 234Pa |
1.17E+00 |
min |
7.02E+01 |
b- |
1.252E+09 |
1.236E+07 |
3.340E-04 |
2.197 |
| 234U |
2.48E+05 |
years |
7.82E+12 |
a |
1.395E+20 |
1.236E+07 |
3.340E-04 |
4.859 |
| 230Th |
7.70E+04 |
years |
2.43E+12 |
a |
4.330E+19 |
1.236E+07 |
3.340E-04 |
4.770 |
| 226Ra |
1.60E+03 |
years |
5.05E+10 |
a |
8.997E+17 |
1.236E+07 |
3.340E-04 |
4.871 |
| 222Rn |
3.82E+00 |
days |
3.30E+05 |
a |
5.885E+12 |
1.236E+07 |
3.340E-04 |
6.681 |
| 218Po |
3.05E+00 |
min |
1.83E+02 |
a |
3.263E+09 |
1.236E+07 |
3.340E-04 |
6.115 |
| 214Pb |
2.68E+01 |
min |
1.61E+03 |
b- |
2.867E+10 |
1.236E+07 |
3.340E-04 |
1.024 |
| 214Bi |
1.98E+01 |
min |
1.19E+03 |
b- |
2.118E+10 |
1.236E+07 |
3.340E-04 |
3.272 |
| 214Po |
1.62E+02 |
Ásec |
1.62E-04 |
a |
2.889E+03 |
1.236E+07 |
3.340E-04 |
7.833 |
| 210Pb |
2.23E+01 |
years |
7.03E+08 |
b- |
1.254E+16 |
1.236E+07 |
3.340E-04 |
3.792 |
| 210Bi |
5.01E+00 |
days |
4.33E+05 |
b- |
7.723E+12 |
1.236E+07 |
3.340E-04 |
5.037 |
| 210Po |
1.38E+02 |
days |
1.20E+07 |
a |
2.132E+14 |
1.236E+07 |
3.340E-04 |
5.407 |
| 206Pb |
stable |
|
Sum 238U Activity for 1 kg Natural Uranium |
|
|
|
Table 1B: Actinium decay series
| Isotope |
Half-life |
Half-life
Units |
Half-life
Seconds |
Decay |
(mole/kg)*
%Abundance at Equilibrium |
Calculated
Activity (Becquerel)
Kg-sec |
Calculated
Activity (Curie) Ci/Kg-sec |
Decay
Energy (MeV) |
| 235U |
7.04E+08 |
years |
2.22E+16 |
a |
1.845E+22 |
5.762E+05 |
1.557E-05 |
4.679 |
| 231Th |
2.55E+01 |
hours |
9.18E+04 |
b- |
7.632E+10 |
5.762E+05 |
1.557E-05 |
4.213 |
| 231Pa |
3.25E+04 |
years |
1.02E+12 |
a |
8.521E+17 |
5.762E+05 |
1.557E-05 |
5.149 |
| 227Ac |
2.18E+01 |
years |
6.87E+08 |
b- |
5.716E+14 |
5.762E+05 |
1.557E-05 |
5.042 |
| 227Th |
1.85E+01 |
days |
1.60E+06 |
a |
1.329E+12 |
5.762E+05 |
1.557E-05 |
6.146 |
| 223Ra |
1.14E+01 |
days |
9.85E+05 |
a |
8.189E+11 |
5.762E+05 |
1.557E-05 |
5.979 |
| 219Rn |
4.00E+00 |
sec |
4.00E+00 |
a |
3.326E+06 |
5.762E+05 |
1.557E-05 |
8.130 |
| 215Po |
1.78E+00 |
msec |
1.78E-03 |
a |
1.480E+03 |
5.762E+05 |
1.557E-05 |
7.526 |
| 211Pb |
3.61E+01 |
min |
2.17E+03 |
b- |
1.801E+09 |
5.762E+05 |
1.557E-05 |
1.373 |
| 211Bi |
2.13E+00 |
min |
1.28E+02 |
a |
1.063E+08 |
5.762E+05 |
1.557E-05 |
6.751 |
| 207Tl |
4.77E+00 |
min |
2.86E+02 |
b- |
2.380E+08 |
5.762E+05 |
1.557E-05 |
1.423 |
| 207Pb |
stable |
|
Sum 235U Activity for 1 kg Natural Uranium |
6,337,932 |
1.713E-04 |
|
Table 2: Thorium decay series
| Isotope |
Half-life |
Half-life
Units |
Half-life
Seconds |
Decay |
N
(kmol) |
Calculated
Activity (Becquerel)
Kg-sec |
Calculated
Activity (Curie) Ci/Kg-sec |
Decay
Energy (MeV) |
| 232Th |
1.40E+10 |
years |
4.42E+17 |
a |
2.596E+24 |
4.075E+06 |
1.101E-04 |
4.083 |
| 228Ra |
5.80E+00 |
years |
6.93E+11 |
b- |
4.072E+18 |
4.075E+06 |
1.101E-04 |
5.520 |
| 228Ac |
6.10E+00 |
hours |
2.20E+04 |
b- |
1.291E+11 |
4.075E+06 |
1.101E-04 |
2.127 |
| 228Th |
1.90E+00 |
years |
5.99E+07 |
a |
3.523E+14 |
4.075E+06 |
1.101E-04 |
5.520 |
| 224Ra |
3.60E+00 |
days |
3.11E+05 |
a |
1.829E+12 |
4.075E+06 |
1.101E-04 |
5.789 |
| 220Rn |
5.50E+01 |
sec |
5.50E+01 |
a |
3.234E+08 |
4.075E+06 |
1.101E-04 |
0.800 |
| 216Po |
1.50E-01 |
sec |
1.50E-01 |
a |
8.820E+05 |
4.075E+06 |
1.101E-04 |
6.906 |
| 212Pb |
1.06E+01 |
hours |
3.82E+04 |
b- |
2.244E+11 |
4.075E+06 |
1.101E-04 |
0.574 |
| 212Bi |
6.10E+01 |
min |
3.66E+03 |
b-,a |
2.152E+10 |
4.075E+06 |
1.101E-04 |
2.254 |
| 212Po |
3.00E-01 |
sec |
3.00E-01 |
a |
1.764E+06 |
4.075E+06 |
1.101E-04 |
8.954 |
| 208Tl |
3.00E+00 |
min |
1.80E+02 |
b- |
1.058E+09 |
4.075E+06 |
1.101E-04 |
5.001 |
| 208Pb |
stable |
|
|
Sum 232Th Activity for 1 kg Natural
Thorium |
44,824,572 |
1.211E-03 |
|
Table 3: Other Significant Isotopes
| Isotope |
Half-life |
Half-life
Units |
Half-life
Seconds |
Decay |
N
(kmol) |
Calculated
Activity (Becquerel)
Kg-sec |
Calculated
Activity (Curie) Ci/Kg-sec |
Decay
Energy (MeV) |
| 40K |
1.28E+09 |
years |
4.03E+16 |
EC,
b- |
1.762E+21 |
3.032E+04 |
8.194E-07 |
1.400 |
| 40Ca |
Stable (89.28%) |
| 40Ar |
Stable (10.72%) |
| |
| 176Lu |
4.00E+10 |
years |
1.26E+18 |
b- |
8.830E+22 |
4.851E+04 |
1.311E-06 |
1.193 |
| 176Hf |
Stable |
| |
| 187Re |
4.35E+10 |
years |
1.37E+18 |
b- |
2.016E+24 |
1.019E+06 |
2.753E-05 |
0.003 |
| 187Os |
Stable |
| |
| 87Rb |
4.75E+10 |
years |
1.50E+18 |
b- |
1.927E+24 |
8.913E+05 |
2.409E-05 |
0.003 |
| 87Sr |
Stable |
| |
| 147Sm |
1.06E+11 |
years |
3.34E+18 |
a |
6.146E+23 |
1.274E+05 |
3.444E-06 |
0.003 |
| 143Nd |
Stable |
|
|

